시계열 데이터란
- 시계열 데이터는 관측치가 시간적 순서를 가지는 데이터를 뜻한다.
- 과거의 데이터를 통해 현재, 그리고 미래를 예측하는데 사용한다.
- 시간에 따라 어떻게 움직이는지에 대해 과거의 자료를 가지고 예측한다.
1. 시계열 데이터의 종류
- 추세변동
- 계절변동
- 순환변동
- 불규칙 변동
1) 추세변동
- 시계열의 장시간에 걸친 지속적인 변화 상태를 나타낸 것이다.
- 시간이 흐른 정도에 따라 자료들의 상승/하향경향 상태를 의미한다
2) 계절변동
- 시계열 자료들을 1년 단위, 혹은 그보다 짧은 단위 기간으로 기록하였을 때, 자연/사회적인 조건, 제도 등의 영향에 따라 계절적인 차이를 나타낸 것이다.
- 주기적인 패턴을 가지고 반복적으로 나타난다.
- 분기별, 월별 자료에서 나타난다.
3) 순환변동
- 몇년간의 간격을 두고 상승/하락이 주기적으로 나타나는 변동이다.
- 계절변동으로 설명되지않는 장기적인 변동이다.
4) 불규칙 변동
- 특수한 사건에 의해 파생되는 변동(천재지변 등)
- 명확한 요인이 없이 발생하는 우연한 변동이다.
2. 시계열 데이터 알고리즘
- 자세한 알고리즘 방식은 추후에 다시 작성하고 우선 어떠한 방식으로 진행되는지 알아보았다.
1) 이동 평균(Moving Average)
- 최근 m개의 관측치를 이용하여 평균을 구하고 이를 통해 예측을 하는 기법이다.
- 데이터 전반에 걸쳐 평균적인 추세를 설명한다.
A) 일방적 이동 평균
- 각 평균에 대한 현재, 그리고 과거의 관측이 포함된다.
- 길이가 7인 시간 X의 이동평균 수식은 다음과 같다.


B) 중심 이동 평균
- 지정된 시점에서 과거 혹은 미래 관측 내용을 계산하는 방식이다.
- 양방향으로 둘러싸는 관측을 사용한다. 양면 이동 평균이라고도 부른다.
- 길이가 7인 시간 X의 중심 이동 평균 수식은 다음과 같다.
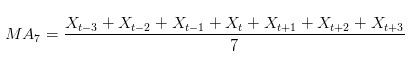

- 이 때, 중심 이동 평균은 중심값을 기준으로 전후에 동일한 양의 관측을 허용하기 때문에 홀수 관측 수에 대해 균등하게 작용한다.
- 따라서 짝수의 경우에는 다르게 적용한다.
- 길이가 8인 시간 X의 중심 이동 평균 수식은 다음과 같다.

C) 이동 평균의 예
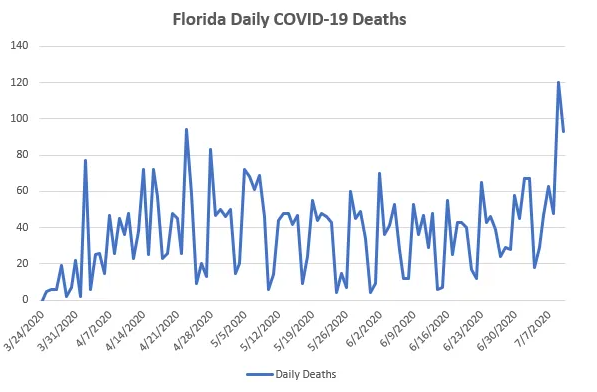
- 코로나 바이러스로 인한 사망인원을 일주일 간격으로 측정한다.
- 사망원인에는 시간적인 요인보다, 인간의 일정요소를 반영해야한다.
- 일주일 중 최저 사망일은 일요일이며 주말은 일반적으로 낮은경향이 있다.
- 화요일은 종종 가장 높은 사망일을 보인다.
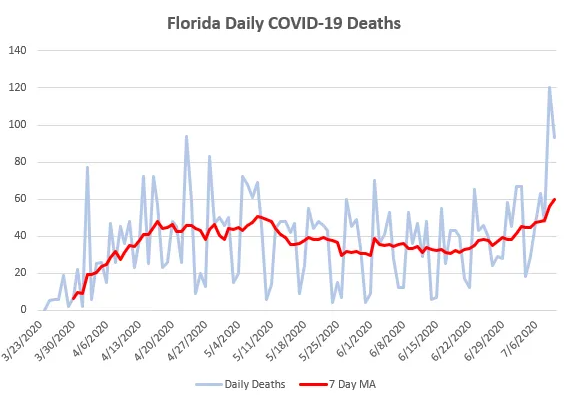
- 각 이동의 평균점은 일주일의 일일 평균점이다.
위와 같이 데이터에 대한 간단한 시각적인 평가를 볼 수 있다. 간단하지만 매우 효과적인 방식이다.
m의 값이 작을수록 최근의 관측치만을 사용하기 때문에 지엽적인 변화에 빠르게 반응 할 수 있다.
2. 다변량 시계열 데이터 (Multivariate Time Series Data)
- 각 시간마다 여러 개의 값을 가지는 데이터를 말한다.
- 시간의 단위는 hour, minute, second, year, month, 등의 단위를 가진다.
- 일정시간동안 간격을 두고 특정변수의 다변량 벡터를 추출하여 쌓음으로 얻어지는 데이터이다.

# Pandas / Numpy / bprophet 등의 필요한 사항을 학습한 후 예측결과를 한번 분석해보고 싶다.
전체적인 내용을 찾아보았지만 수식부분에선 아직까지 한번에 눈에 들어오지 않았다.
'IT > Algorithm' 카테고리의 다른 글
| DFS / BFS (0) | 2021.06.02 |
|---|---|
| 완전탐색 / 이분탐색 (0) | 2021.05.31 |
| STACK / QUEUE (0) | 2021.05.17 |
